INECUACIONES CUADRÁTICAS
Las matemáticas son la música de la razón
OBJETIVO

Al concluir esta lección, deberás ser capaz de:
- Hallar la solución de inecuaciones de forma: ax 2 + bx +c < 0
- Expresar las soluciones de inecuaciones en forma de intervalo o como conjunto.
- Trazar en la recta real la solución.
- Usar métodos de solución, de manera lógica y sistemática.
INTRODUCCIÓN
Las inecuaciones cuadráticas son desigualdades donde la variable tiene el exponente 2 , igualándolo a cero. Resolver una inecuacion es encontrar el conjunto de números reales (intervalo).
Como resolver una inecuacion cuadrática:
Existen tres pasos según su discriminante:
Como resolver una inecuacion cuadrática:
Existen tres pasos según su discriminante:
- Discriminante Positivo: Cuando la ineacucion tiene dos soluciones reales distintas.
- Discriminate Cero: La inecuacion tiene una solución real doble.
- Discriminante Negativo: La ecuación no tiene solución real. Por lo tanto, el signo del trinomio es el mismo que el de coeficiente a.

¿QUE ES UNA INECUACION CUADRÁTICA?
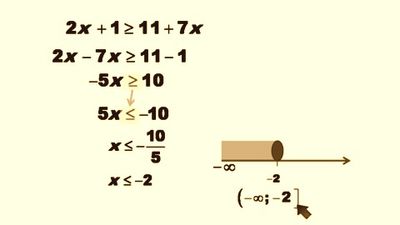
PROPIEDADES BÁSICAS
A continuación vamos a observar algunas de las propiedades de las desigualdades (y de las inecuaciones). Vamos a ver dos propiedades básicas que cumplen las desigualdades y por consiguiente las inecuaciones.
Propiedad 1: Los números A y B siempre cumplen una de las siguientes afirmaciones:
Propiedad 2: Esta propiedad se refiere a la simetría de las inecuaciones o desigualdades:
Propiedad 1: Los números A y B siempre cumplen una de las siguientes afirmaciones:
- A< B
- A= B
- A> B
Propiedad 2: Esta propiedad se refiere a la simetría de las inecuaciones o desigualdades:
- A< B => B> A
- A> B => B< A

EJERCICIOS PROPUESTOS
Halla la solución de las siguientes inecuaciones cuadráticas y representarla en la recta numérica.
- 6x2 + 7x ≤ 3
- x2 – 2x – 80
- x2 + 5x - 6 ≥ 0
- x2 – 7x ≤ -6







